AIPT Section 4.2: CFR – Game Abstractions

CFR - Game Abstractions

Abstraction is the main method for solving incomplete information games that are too large to be solved in their original form. It is extremely prevalent in solving poker games.

Game Abstraction Techniques

The Abstraction-Solving-Translation model includes the following steps:

First, the game is abstracted to create a smaller game that is strategically similar to the original game. Then the approximate equilibrium is computed in the abstract game, and finally the abstract game is mapped back to the original game. The resulting strategy is a Nash equilibrium approximation in the original game, but will still be exploitable to some degree since it is only an actual Nash equilibrium in the abstracted smaller game.

We need abstraction when game sizes are too large to be solved with current technology, or when the original game may be too difficult or large to write in full details, or when the game may not be composed of discrete actions/states in its original form.

Strategies for abstract games are defined in the same way as strategies in the main game, but restricted strategies must be given zero probability, meaning if there was a betting abstraction to use only check, bet 1/2 pot, and bet full pot, in a situation where the pot is \$100, only checking, betting \$50, and betting \$100 would be possible, while all other options would be given zero probability.

Game Size

The size of a game is generally computed from two components:

1. The number of game states, which is generally counted as information sets in poker to account for situations that are equivalent given one player’s information, and therefore which the player uses the same strategy for each information set
2. The number of actions at each of these information sets

The composite multiplication of these two components is referred to as infoset actions, which is related to the amount of memory needed to store a strategy, like in the CFR algorithm. This is the standard game size measurement in poker.

The size of a game is valuable because it lets us relate complexity of different games and determines which algorithms might be usable and what level of abstraction might be needed to get a game complexity to a tractable level.

Michael Johanson wrote a paper Measuring the Size of Large No-Limit Poker Games in 2013 that explains these methods in detail.

This can be extended by considering the game states from multiple perspectives. The two-player view is in terms of an external players view of the number of infoset-actions (they cannot see private cards). The one-sided view is as described above, with one player’s infoset-actions. The canonical one-player view further reduces the size by including lossless abstractions (states that are strategically identical).

CFR stores regrets and strategies at each information set, so CFR is known to run in proportion to the size of the game.

Limit Hold’em Size

In limit hold’em, the task of computing the number of infoset-actions is relatively easy because there is only one betting option allowed for each betting round, which can only occur a maximum of four times, and the betting actions and information sets within each round are independent of the betting history and stack sizes (assuming large enough stack sizes to be able to complete all bets). From a one-player perspective (assuming the 2nd player’s cards are unknown), the number of ways to deal the cards is calculated as:

52c2 for the 1st round and then 52c2 * 50c3 for the 2nd round, and so on

These calculations would be reduced if we considered lossless abstraction of card combinations.

We can calculate the number of information sets by looking at each round and multiplying the card combinations in that round by the possible betting sequences based on a chart of betting sequences.

No Limit Hold’em Size

No-limit poker is more of a computational challenge because each betting round depends on prior rounds, since each player’s stack size varies as the hand progresses. Each game depends on two variables: the stack size to start the game and the value of the big blind.

Per the game rules, players have the following two betting restrictions: Minimum bet: max(big blind, current bet size) Maximum bet: Stack size

The legal actions possible depend on three factors: “amount of money remaining, size of bet faced, and if it’s possible to check (if it’s the first action in a round)”.

Each of these factors strictly increases or decreases in a round. The method used to compute the number of infoset-actions in no limit hold’em poker is to “incrementally compute the number of action histories that reach each of these configurations by using dynamic programming”.

Michael Johanson’s paper performs these calculations for the standard No Limit Texas Hold’em game used in the ACPC, which uses \$20,000 (200-blind) stacks with \$50- \$100 blinds. Although 200 blinds is fairly normal in poker (although most online games start with 100 blinds), the large stack size in absolute dollar terms means that a much larger number of actions are possible than, for example, 200 blinds in a \$1-\$2 blind setting. The initial raise in the latter setting is any amount from \$4 to \$400, whereas in the former it is \$200 to \$20,000.

Comparing Limit and No Limit Hold’em

Whereas limit hold’em has a 1-sided canonical game size of 1.4x10^13 infoset actions, no limit \$1-2 with \$1000 starting stacks (500 blinds) is 3.12x10^71, \$1-2 with \$400 (\200 blind) starting stacks is 6.0x10^46, and \$50-100 with \$20,000 (200 blind) starting stacks is 2.8x10^160. Not including transpositions, chess has 10^47 game states, checkers has 10^20 game states, and Go has 10^170 states.

Although one vs. one limit hold’em has now been solved over a long computation period with a very specialized parallel machine setup, no limit is substantially larger and requires abstraction to make the game small enough to be solved.

Johanson recommends finding a game that is able to be analyzed in unabstracted form but that is still valuable as a research test experiment. He suggests that the game should be compatible with three properties:

1. “Unabstracted best response computations are tractable and convenient, so worst case performance of strategies with abstracted betting can be evaluated. One can then evaluate abstraction and translation techniques in isolation from other factors.”

2. “Unabstracted equilibrium computations are tractable and convenient. So we can compute an optimal strategy for the game and measure its performance against agents that use betting abstraction.”

3. “Strategic elements similar to those of NLHE” (in terms of rounds, deck size, 5- card poker hands, and large stack sizes)

Properties (1) and (2) allow for us to compare agents in the full game and in terms of (1) best response and (2) against the full game equilibrium. For condition (3), in order to provide the flexibility of solving this game on standard personal computers, we are limited in the size of the game that we can possibly use, but essentially meeting the first two properties and making the game as large as possible would be most valuable to be as strategically close to NLHE as possible.

Royal No Limit Hold’em

Johanson suggests a potential testbed game as 2-\$20 \$1-\$2 No Limit Royal Hold’em, a game which uses 2 betting rounds, \$20 stack sizes, and \$1-\$2 blinds. The game size is 1.55x10^8 and CFR requires 7GB of RAM for the computation.

While the size of full poker games that are commonly played in casinos require more memory than is feasible for today’s modern computers, Royal No Limit Hold’em is accessible to all, which could make a game of this sort a more even playing field in a competition. Later on this page, we show an experiment with this game to evaluate different betting abstractions and show that unfortunately the game may be too small to work effectively.

With more advanced CFR versions that use deep learning rather than only tabular data like the original CFR, it’s likely that a much larger testbed game could be explored now in 2021.

Types of Abstractions

The two main ways to create a smaller game from a larger one in poker are to merge information sets together (card abstraction) and to restrict the actions a player can take from a history (action abstraction). These techniques are often combined.

A further possibility is to simplify the game itself. This can be done in poker by limiting the maximum number of bets per round, eliminating betting rounds, and eliminating cards. For example, the variant of Texas Hold’em that we analyze with betting abstractions below is called Royal Texas Hold’em and uses only 20 cards instead of the standard 52 in the deck.

Abstractions can be either lossless or lossy. A lossless abstraction respects the original strategic complexity of the game, while reducing the number of game states.

Lossless Abstraction and Isomorphisms

With poker, the first step is usually to use lossless abstraction to take advantage of the strategic equivalence of poker hands with regards to their suits. All suits are of the same value, so only how many cards of the same suit a player has is relevant, not the actual type of suit. For example, a player with a starting hand of Jack of spades and Queen of hearts has the same exact quality hand in the case of having Jack of diamonds and Queen of clubs. There are 16 combinations of a Queen and Jack. The 12 that are different suits can be reduced to only one abstracted strategy and the four of the same suit are also equivalent to one abstracted strategy. Such abstractions generally reduce the size of poker games by one to two orders of magnitude. Lossless abstraction enabled the solution of Rhode Island Hold’em (by Gilpin and Sandhol from CMU in the mid 2000s), an AI challenge problem with 3.1 billion nodes in the game tree, but generally, lossy abstraction is also needed.

This lossless abstraction must be redefined at each betting round, because while the type of suits are not relevant on a per-round basis, future rounds can redefine the value of a hand according to its suits. Continuing the above example, after a flop of 6h7h8h, the QhJs hand is much superior to the QcJd hand due to now having four hearts (one heart away from a flush).

In a Texas Hold’em game, just from the first round alone, we move from 52c2*50c2 = 1,624,350 to 28,561 combinations by using lossless abstraction.

Kevin Waugh showed a fast and optimal technique to index poker hands that accounts for suit isomorphisms. Isomorphisms are cases where poker hands cannot be strategically distinguished. Using such techniques, we can build lossless abstraction. For example, in Royal Hold’em, where there are 20 cards (four suits and cards Ten, Jack, Queen, King, and Ace), we have the following two-card starting hands:

• Order and suitedness matter: 20 ∗ 20 = 400 combinations
• Order does not matter, suitedness matters: 20c2 = 190 combinations
• Order and suitedness do not matter: 25 combinations (10 unpaired combinations both suited and unsuited and 5 pairs)

We can permute the suits and order of the cards within any round however we would like without losing any strategic significance, so Royal Hold’em effectively begins with only 25 information sets for the player acting first in the preflop round. According to Waugh’s paper, it is important that we can construct an indexing function that is efficient to compute which is optimal with no holes, has an inverse mapping, and is generalizable to other games.

In practice, we store the regrets and strategies for each index, whereby multiple equivalent hands can use the same index. The indexing procedure works by indexing using the multiset-colex index, whereby we first index rank sets (sets of cards of the same suit), then rank groups (sequences of rank sets), and finally combine them into a hand index (details in the paper linked above).

Lossy Abstraction

All other abstractions are lossy and result in some loss of strategic significance. We look at experiments with action abstraction in our work with Royal No Limit Hold’em and with card abstraction in Kuhn Poker.

Action abstraction is when players are given fewer actions available than in the original game, that is, a restriction on the players’ strategy space. This is especially useful for games with large numbers of possible actions available, such as NLHE. In no limit poker, the most standard action abstraction is allowing only {fold, call, pot bet, allin bet}. This restricts the first action in a no limit hold’em game with \$20 starting stacks and a \$2 big blind to either {fold, call \$2, raise to \$4, raise to \$20} instead of {fold, call, raise to any amount between and including \$4-\$20}, which results in four total actions possible instead of 19. These types of abstractions are often used when running solver simulations.

Card, or information, abstraction occurs by grouping categories of hands into equivalence classes called buckets. The standard method, expected hand strength, works by grouping by the probability of winning at showdown against a random hand by enumerating all possible combinations of community cards and finding the portion of the time the hand wins. For example, one could create five buckets to divide the probabilities into equities from {0-0.2, 0.2-0.4, 0.4-0.6, 0.6-0.8, 0.8-1}. This could lead to some buckets being very small and others very large. Hands also must transition between buckets during play. Buckets could be created automatically such as in the manner just described or manually, which requires expert input, but would be quite difficult to create policies for.

Three common ways of bucketing are:

Expectation-based: Developed by Gilpin and Sandholm in 2007. Buckets are created based on the potential to improve given future cards, potentially by putting the same amount of hands into some fixed number of buckets according to hand strength. A problem is that buckets can be unevenly distributed and that there are often strategic differences in playing draw hands compared to made hands, which would not be differentiated here (for example the expectation of the value of JT on 983 may be similar to A8, but the A8 is a mid strength hand that probably should be playing passively and the JT is a good semi bluffing hand that has overcards and a straight draw). The standard technique is to make each bucket on each round to have the same percentage of cards based on a hand strength measure, which could be based on the expectation of hand strength E[HS] or E[HS^2] (gives more value to hands with higher potential to improve in the future) or some similar metric, which are measured against winning at showdown against a random hand.

Potential-aware: Automated abstraction technique that was created in 2007 by Gilpin and Sandholm that uses multi-dimensional histograms, where the maximum number of buckets in each round is determined based on the size of the final linear program to solve. This starts in the final round by bucketing hands into sets with k-means clustering and then buckets on prior rounds are derived from the final round based on how often they turn into the final round clusters. So if there are five clusters on the final round, then there would be a distribution of five transition probabilities on the prior round, which are then grouped together using some similarity function such as Euclidean distance for each value in the histogram. This continues backwards until the first round.

Phase-based: This method solves earlier parts of the game separately from later parts of the game, which allows for finer abstraction in each segment than would be possible in the game as a whole.

Additionally, most poker algorithms depend on perfect recall in terms of theory to arrive at a Nash equilibrium. This is the assumption that an agent doesn’t forget anything and can rely on prior knowledge. An additional way to abstract, then, is to use imperfect recall abstractions (which remove theoretical CFR guarantees), which are when the player “forgets” previous observations and uses information based only on specific parts of the history, or even on no history at all. This assumption is therefore not very applicable to real life, although in real life the true human memory does not remember all of the historical observations and actions like in perfect recall abstractions.

Imperfect recall therefore places more emphasis on recent information, which can be done by using an abstraction with fewer buckets on earlier rounds or by forgetting all prior rounds except for the current. This is similar to endgame solving – a way to focus resources on the most important betting rounds and decisions, particularly in no limit hold’em.

There are three main methods to compare abstraction solutions to poker games: one on one (against either another agent or a human), versus equilibrium, and versus best response. Respectively, the possible problems possible are intransitivities, infeasible computation, and not being well correlated with best performance. Abstractions can also be measured based on their ability to estimate the true value of the game.

Action Translation

A reverse mapping, also known as action translation, is used to map actions in the original game, where all actions are possible, to an action in the abstracted model. This is necessary because opponents can take actions in the full game that have been removed from the abstracted model. Clever bet sizing can render the most basic mappings highly exploitable. An intelligent model is needed to handle these situations. The basic model works by mapping an observed action a of the opponent to an action a’ that exists in the abstracted model, and then responding to the action as if the opponent had played a’.

Prior to Ganzfriend and Sandholm’s solution in 2013 in “Action Translation in Extensive-Form GAmes with Large Action Spaces: Axioms, Paradoxes, and the Pseudo-Harmonic Mapping”, most mappings were exploitable and based on heuristics, not theory.

Their model works as follows: The opponent bets x, an element of [A, B], where A is the largest betting size in the abstraction that is ≤ x and B is the smallest betting size in the abstraction that is ≥ x, assuming 0 ≤ A < B.

The question is where to match (and therefore respond to) the bet x as if it were A or B. f_{A,B}(x) is the probability that we map x to A with the goal being to minimize exploitability.

The following basic desiderata properties are given for all action mappings in poker from the paper:

1. Boundary Constraints: If an opponent bets an action in our abstraction, then x should be matched to that bet size with probability 1, so f(A) = 1 and f(B) = 0.
2. Monotonicity: The probability mapping to A should decrease as x moves closer to B
3. Scale Invariance: Scaling A, B, and x by some multiplicative factor k > 0 does not affect the action mapping
4. Action Robustness: Such that f changes smoothly in x, avoiding any sudden changes that could result in exploitability
5. Boundary Robustness: Such that f changes smoothly with A and B

There are also properties that are justified based on a small toy game called the clairvoyance game, found in the book The Mathematics of Poker. The game works as follows:

• Player P2 is given no private cards
• Player P1 is given a single card drawn from a distribution of half winning and half losing hands
• Both players start with n chips
• Both players ante \$0.50, so the starting pot is \$1
• P1 acts first and can bet any amount from 0 to n
• P2 responds by calling or folding (no raising is allowed and a bet of 0 simply results in a showdown)

The solution of this game was found to be:

• P1 bets n with probability 1 with a winning hand
• P1 bets n with probability n/(1+n) with a losing hand (otherwise checks, with probability 1/(1+n))
• P2 calls a bet of size x ∈ [0, n] with probability 1/(1+x)

This motivates the proposed action translation mapping of, which meets the above desiderata and that is consistent with the results of the clairvoyance game:

f_{A,B}(x) * 1/(1+A) + (1-f_{A,B}(x))*1/(1+B) = 1/(1+x)

Which can be solved to find the mapping, called the pseudo harmonic mapping:

f_{A,B}(x) = (B-x)(1+A)/((B-A)(1+x))

This mapping is the only one consistent with player 2 calling a bet size of size x with probability 1/(1+x) for all x ∈ [A, B].

This mapping exhibited less exploitability than prior mappings in almost all cases, based on test games such as Leduc Hold’em and Kuhn Poker. In Kuhn Poker, an interesting phenomenon was discovered – that fitting an action betting abstraction to a known equilibrium strategy could actually result in the agent being more exploitable. The optimal bet size was found to vary significantly as different stack sizes and mappings were used.

This means that the optimal action abstraction to use could vary depending on the action translation mapping used. It may be important to use action abstractions that are a combination of optimal offensive actions used by the agent itself and defensive actions that are used by opponents and are necessary to reduce exploitability. It may be even better to use game specific information in determining abstraction or to use different mappings at different information sets.

Card Abstraction in Kuhn Poker

For this coding project, we use a verison of Kuhn Poker with deck size of 100 cards, so the game still has the same rules, but the complexity increases as players do not have such simplistic decisions as they would with a very small deck. Kuhn Poker has only four information sets per card, so it has 12 information sets in standard form (using 3 distinct cards) and 400 information sets in the 100-card version.

We compared these versions of CFR:

1. Chance Sampling (sampling only chance nodes and then running regular CFR)
2. External Sampling (sampling chance nodes and opponent nodes)
3. Vanilla (regular)
4. CFR+ (regular CFR with a modified regret metric that resets regrets to 0 if they become negative)

For the External and Chance Sampling CFR versions, we tested simple bucketing that splits the cards into three, 10, and 25 buckets. This means that with 3-bucket abstraction, each group of hands {0-32, 33-65, 66-99} will share a single strategy. Essentially each player’s card is hidden to himself and he only knows which bucket his card is in, although at showdown, each player’s true card would be shown to determine the winner of the hand.

The results are shown below. Again, the game values for all abstractions are -0.0566 except for the 3-bucket abstraction, which is -0.0264, meaning that the Player 2 advantage is decreased due to the weakness of the abstraction. Note that ES and CS refer to External Sampling and Chance Sampling and 3B/10B/25B refer to 3 buckets, 10 buckets, and 25 buckets.

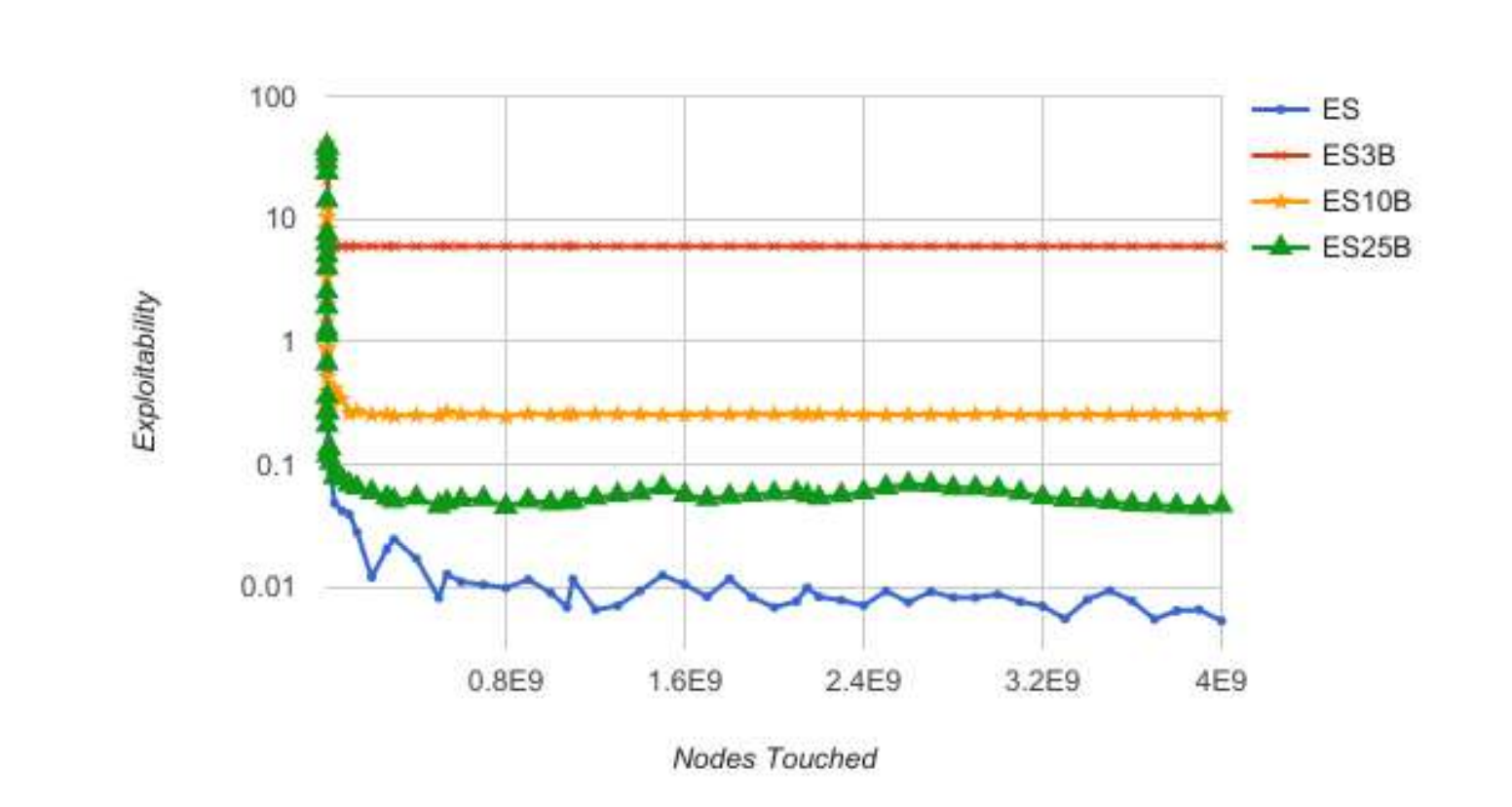
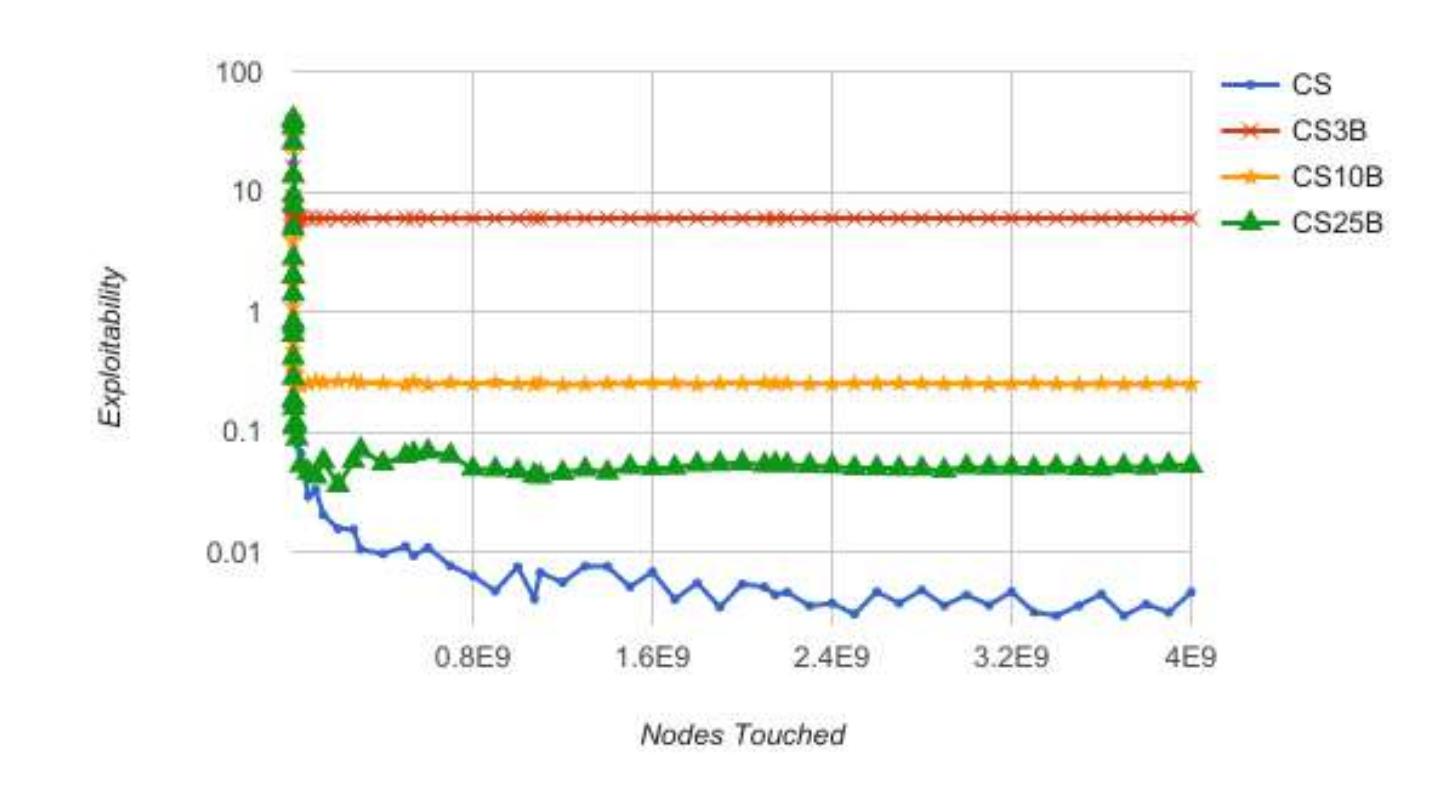
The figures are quite similar for both algorithms and show that the lower bucket abstractions converge slightly faster than the 25-bucket abstraction, which is also faster than the unabstracted exploitability. However, the unabstracted exploitability is almost immediately less exploitable than the alternatives, rendering them not very useful, probably because the game is not complex enough. We also see here that the exploitability values are significantly better as the number of buckets increases, because with fewer buckets, more hands share the same strategy.

Bet Abstraction in No Limit Royal Hold’em

We look a variation of No Limit Hold’em called Royal No Limit Hold’em that requires only 7GB of RAM to solve (assuming one byte per infoset to store the behavioral strategy and two 8-byte doubles per infoset to solve the game precisely), which means that it can be used as a testbed for anyone to work on, without requiring access to supercomputers. This game and its use as a testbed was given as an idea by Michael Johansen in his 2013 paper, “Measuring the Size of Large No-Limit Poker Games”and was described above in the Royal No Limit Hold’em section. This testbed concept was important because at the time, during the ACPC, a major factor correlating to the quality of the poker agents was access to powerful supercomputers capable of solving larger game abstractions, which gives an advantage to those with access to such machines.

Royal No Limit Hold’em is a simplified version of No Limit Texas Hold’em. We will study the game with 2 players, blinds of \$1 (small blind) and \$2 (big blind), and starting stacks of \$20 per player, which reset after each hand. Instead of a standard 52 card deck, the Royal game means that we discard cards 2 through 9 and use only the Ten, Jack, Queen, King, and Ace, hence the name Royal. Royal Hold’em has only two betting rounds, not four as in standard Texas Hold’em. There is the preflop round and then after the flop (the first three community cards) betting round, the Royal Hold’em game ends. No limit betting is the same as in Texas Hold’em – no maximum number of bets per round and the minimum bet is the big blind or the prior bet/raise size, whichever is larger. The maximum bet size is the amount of chips in front of each player.

The strength of hands in Royal Hold’em is, in order from best to worst: Royal flush (the only flush possible), Four of a kind, Full house, Straight, Three of a kind, Two pair, One pair (worse hands are not possible). In normal poker, a hand without pairs would be possible and also other flushes would be possible.

Royal No Limit Hold’em has on the order of 10^8 information sets, compared to the full No Limit Hold’em game on the order of 10^161 information sets.

The purpose of experimenting with action abstractions in Royal No Limit Hold’em is to understand which abstractions are most efficient, and since Royal Hold’em has many features in common with Texas Hold’em, it is hoped that these abstraction features could be transferred to researchers studying Texas Hold’em or other incomplete information games.

The experiment was run using the ACPC standard protocol and a version of CFR called Pure CFR created by Richard Gibson of the University of Alberta and Kevin Waugh’s card isomorphism open source code. Pure CFR is a version of CFR that samples pure strategy profiles (exactly one action assigned probability 1 at each state) for each iteration, using no sampling. Pure CFR has been shown to work faster than Vanilla CFR and also is memory efficient by using only integer values and not doubles, which is made possible by the pure strategy profiles and the fact that pot sizes and bets in poker are all integer valued.

We tested solving the full game and also the game with these action abstractions:

1. Fold, call, pot, allin (FCPA)
2. Fold, call, half pot, allin (FCHA)
3. Fold, call, minimum, half pot, pot, allin (FCMHPA)
4. Fold, call, minimum, half pot, three-quarters pot, pot, allin (FCMHQTPA)

Since the full game can be solved completely, this enables us to compare our abstracted solutions against the full game solution, otherwise not possible in standard poker games due to the size of the full game.

Each abstraction and the main game were run for 12 hours over four threads on a 2.6 GHz Intel Core i7 computer with 16 GB of RAM. Since there was not a best response algorithm used in this experiment, the abstractions were run for shorter periods and then tested and then continued for longer periods until it seemed that the strategies had converged, based on the match result changes. The sizes of the strategies of the abstractions from smallest to largest were 5.5 MB, 10.2 MB, 160 MB, and 471 MB. The full game solution is 3.58 GB.

We compare our abstractions in two ways:

1. Against main game equilibrium: Each of the four abstracted solutions plays against the main game solution in the main game
2. Against each other: Each of the four abstracted solutions plays against each other in the main game

After solving the game in the abstracted action space, we must allow for the abstracted player solution to play in the original game, where all actions are allowed.

This requires the use of action translation. As described above, the following translation has been shown to be less exploitable than other options:

f_{A,B}(x) = (B-x)(1+A)/((B-A)(1+x))

Matches between all combinations of the four abstractions and the full game were played over 10,000,000 hands each in duplicate, so 5,000,000 were played once and then the same 5,000,000 were played again with the hands swapped to reduce variance.

The following table lists the results from the perspective of the row abstraction in terms of big blinds per 100 hands (i.e., the number of $2 amounts won per 100 hands):

We see that the full agent dominates all abstracted agents, as expected. FCPA is slightly superior to the other agents against the full agent. FCPA also beats all of the other abstracted agents, which may be due to the more sophisticated ones becoming overfit to their abstracted games. FCHA loses to all abstractions, possibly because the half pot and all-in bets results in too wide of a range between the two actions.

Unfortunately, the relatively small size of the game, intended to provide access to individuals without access to supercomputers, results in the abstracted agents for the first player strategy in the preflop round to virtually always only call the big blind or to go allin. While the full game agent plays a more mixed strategy that involves raising to a variety of sizes, a large amount of these raises are near-all-in amounts, that are strategically essentially equivalent to an all-in bet (e.g., raising to 18 out of 20 chips on the first action).

Waugh et al’s work on abstraction pathologies shows that despite finer abstractions tending to perform better and better each year in the ACPC, these abstractions do not guarantee better results. However, they do show that if the opponent is playing the full game, that the opponents should be monotonically improving as their abstractions grow larger, which we did not see in these results, although the winrates are within only about 2% between the different abstractions. They showed that in abstraction vs. abstraction matches, monotonicity often does not hold, and agents could even become more exploitable. A theory is that providing additional strategies to a player can encourage the player to exploit the limitations of the opponent’s abstraction, resulting in a strategy that is more exploitable by actions that become available to the opponent in the full game.

While these results show evidence of FCPA being the best abstraction amongst these choices – it may be necessary to run this experiment on a larger testbed game that may not be solvable on personal computers, but also does not require very specialized equipment. For example, even doubling the blinds so that each player starts with 20 big blinds instead of 10 would possibly significantly increase the complexity, although in doing so would significantly increase the game size since already on the flop there would be 38 initial actions (fold or raise to any amount between 4 and 40) instead of 18 initial actions (fold or raise to any amount between 4 and 20).